II.5. Rheological measurements
II.5.1. Apparatus
The rheological parameters of fresh mortars can be determined by applying a given shear rate and measuring the resulting shear stress. A Rheometrics Fluid Spectrometer RSF II was used in experimental testing.
The fresh mortar was placed into a cylindrical vessel. The rheometer was equipped with vane geometry to measure the rheological properties of the mortar. Previous experiments showed that the vane was adequate for the characterisation of cementitious systems [34]. However, for some admixed mortars, bleeding phenomena affected the experiments, due to the high water/cement ratio. In consequence, a helical geometry was also used. Both configurations provided minimum gaps around 5 mm. Working within these wide-gap geometries facilitates studying coarse particles (up to 0.5 mm). In addition, there were enough particles in the gap to take into account, so that, the properties of the suspension, viewed as a continuum medium, were measured for all the materials studied. As the cylinder rotated, the viscous resistance of the mortar flowing through the blades generated a torque, which was continuously registered. Using Couette analogy, the calibration was performed with silicon oil for both mobiles [35].
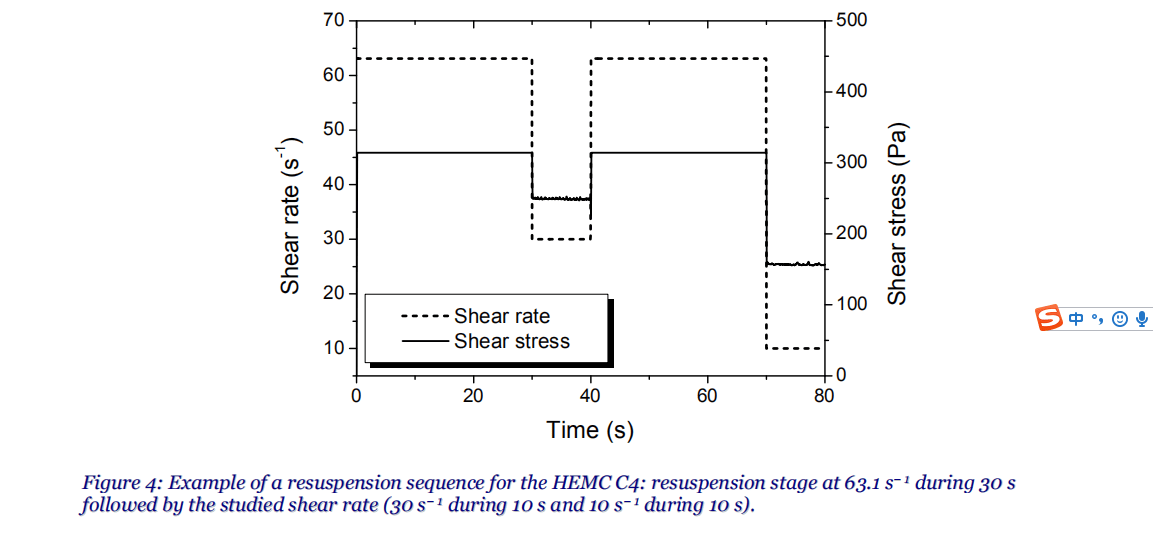
Despite the use of mixing-type geometry, some admixtures remained affected by sedimentation. So, in order to put back in suspension the mortars, the samples were systematically submitted to a high shear rate during few seconds before each imposed shear rate. For each mortar, measurements began 5 min after mixing. The material was pre-sheared
at 63.1 s− 1 during 30 s. This pre-shearing action was intended to create uniform conditions before testing and to limit the effect of sedimentation. Then, the studied shear rate was applied (for example 30 s− 1) during 10 s. An example of the sequence used is depicted in
Figure 4.
II.5.2. Curve modelling
Therefore, in characterizing the fundamental flow properties of a material, the shear stress (τ (Pa)) was plotted versus the shear rate ( .(s− 1)). Yahia and Khayat [36] and Nehdi and Rahman [37] performed tests with various models (Bingham, Herschel–Bulkley, Sisko, modified Bingham, Casson, and De Kee models) and concluded that flow properties depended on both material composition and experimental conditions. Cement pastes and some mortars did not follow the linear function of Bingham's Law. Consequently, an improved model to fit
the flow curves was developed by Herschel and Bulkley [38]. They proposed a power-law variant of the viscoplastic Bingham model. Larrard et al. [39] used this equation (Equation 5) for concretes because it was the most suitable to describe the experimental rheograms.
t =t0 + k g n (5)
τ0 is the yield stress, representing the amount of stress required to initiate or maintain flow. K represents the consistency coefficient (Pa sn), and n is the flow index (no unit). When n = 1, the formula reduces to the Bingham model. The shear-thinning behaviour is associated with 0 < n < 1, and the unusual shear-thickening behaviour with n > 1 [40]. When τ0 << . n K,Equation 5 can be reduced to the power-law model (Equation 6) [41]:
t =t = Kg&n (6)
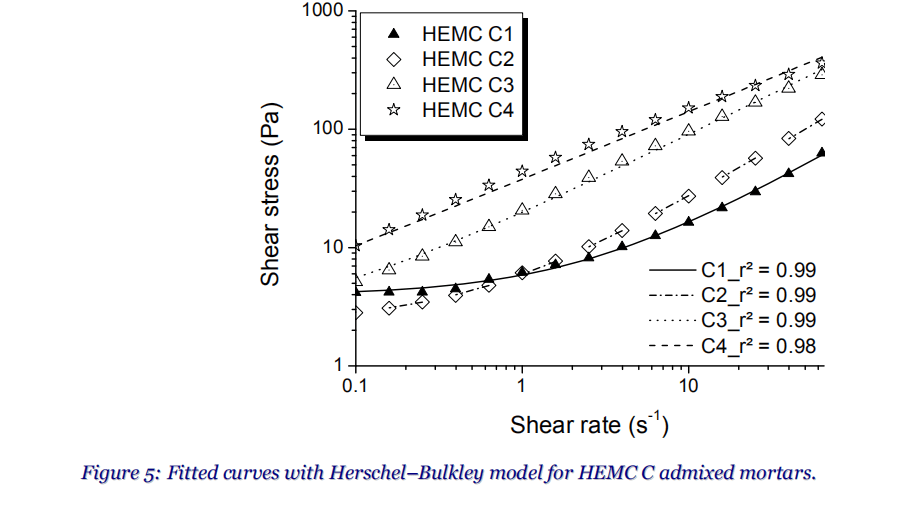
In this paper, the Herschel–Bulkley model was chosen to compare admixtures to each other. Rheograms were fitted with the Herschel–Bulkley model as shown on Figure 5. The coefficients of correlation are next to 0.99 for all the studied mortars.
Reference:
[33] S. Hucko, Hot climate render additive, Proceedings of the V SBTA (Simpósio Brasileiro De Tecnologia Das Argamassas), São Paulo, Brazil (2003).
[34] H.A. Barnes and Q.D. Nguyen, Rotating vane rheometry — a review, J. Non-Newton.Fluid 98 (1) (2001).
[35] A. Ait-Kadi, P. Marchal, L. Choplin, A.S. Chrissemant and M. Bousmina, Quantitative analysis of mixer-type rheometers using the Couette analogy, Can. J. Chem. Eng. 80 (6) (2002).
[36] A. Yahia and K.H. Khayat, Analytical models for estimating yield stress of highperformance pseudoplastic grout, Cem. Concr. Res. 31 (5) (2001).
[37] M. Nehdi and M.-A. Rahman, Estimating rheological properties of cement pastes using various rheological models for different test geometry, gap and surface friction, Cem. Concr. Res. 34 (11) (2004).
[38] W.M. Herschel and R. Bulkley, Measurements of consistency as applied to rubber–benzene solutions, Am. Soc. Test. Mat., Proc. 26 (1926).
[39] F. Larrard, C.F. Ferraris and T. Sedran, Fresh concrete: a Herschel–Bulkley material, Mat. Struct. 31 (7) (1998).
[40] P. Coussot and C. Ancey, Rhéophysique des pâtes et des suspensions, EDP Sci. (1999).
[41] C. Atzeni, L. Massidda and U. Sanna, Comparison between rheological models for portland cement pastes, Cem. Concr. Res. 15 (3) (1985).